This is not the first time i heard Differentiating Instruction as we believe that children develop at different pace. However, from this lesson, I learnt to break down to 3 levels of learners in simple math problem. Not only can we see how one problem can progress from simple to complex, we were also guided to think of follow up activities for the three level of learners.
E Mathematics Newsletter
Sunday 18 August 2013
Day 6 Blog
My take away for this last lesson is Carol Tomlison Differentiating Instruction model is an approach to teaching that advocates active planning for student differences in classrooms.
This is not the first time i heard Differentiating Instruction as we believe that children develop at different pace. However, from this lesson, I learnt to break down to 3 levels of learners in simple math problem. Not only can we see how one problem can progress from simple to complex, we were also guided to think of follow up activities for the three level of learners.
This is not the first time i heard Differentiating Instruction as we believe that children develop at different pace. However, from this lesson, I learnt to break down to 3 levels of learners in simple math problem. Not only can we see how one problem can progress from simple to complex, we were also guided to think of follow up activities for the three level of learners.
Day 5 Blog - Geometry
We were reminded of the different names of triangles such as Scalene, Isosceles and Equilateral triangles in this lesson. When Dr Yeap gave us the first problem: "Show 2 ways of showing 60 degree angle". It took me awhile to verify the ways as i took it for granted that 3 angles of a triangle is 180 degree and each angle is 60 degree. When he questioned "How would you know is 60 degree", i couldn't answer thinking aloud "Isn't it known that each angle in a triangle is 60 degree??"
I like the idea of folding the triangle down so that all angles are in a straight line to be useful.
Today the main problem is:
This problem is tough for me handle. As what Dr Yeap mentioned, I lacked the "visualisation" that allows me to spot angle ADC and CEF to be 162 degrees too. It is a good recap for me to challenge myself!
I like the idea of folding the triangle down so that all angles are in a straight line to be useful.
Today the main problem is:
Types of angles
Acute angle:
An angle whose measure is less than 90 degrees. The following is an acute angle.
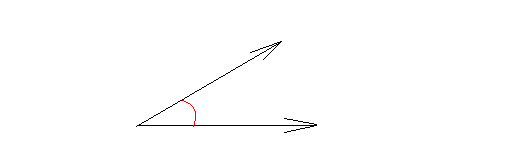
Right angle:
An angle whose measure is 90 degrees. The following is a right angle.
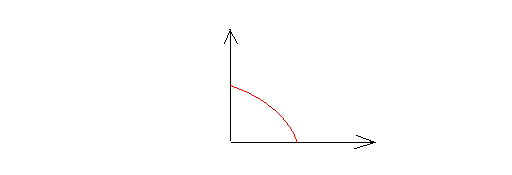
Obtuse angle:
An angle whose measure is bigger than 90 degrees but less than 180 degrees. Thus, it is between 90 degrees and 180 degrees. The following is an obtuse angle.
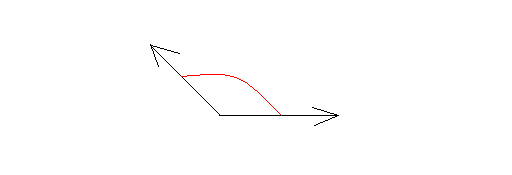
Straight angle
An angle whose measure is 180 degrees.Thus, a straight angle look like a straight line. The following is a straight angle.
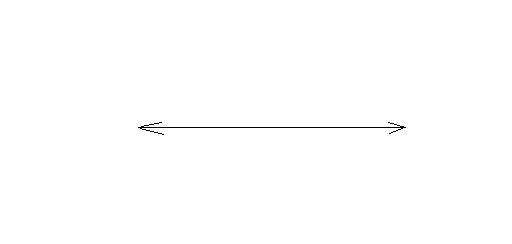
Reflex angle:
An angle whose measure is bigger than 180 degrees but less than 360 degrees.The following is a reflex angle.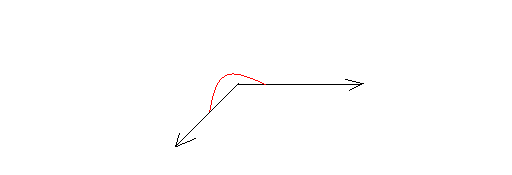
Adjacent angles:
Angle with a common vertex and one common side. <1 and <2, are adjacent angles.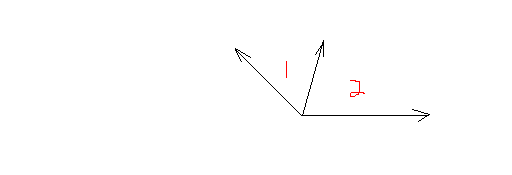
Complementary angles:
Two angles whose measures add to 90 degrees. Angle 1 and angle 2 are complementary angles because together they form a right angle.
Note that angle 1 and angle 2 do not have to be adjacent to be complementary as long as they add up to 90 degrees
Supplementary angles:
Two angles whose measures add to 180 degrees. The following are supplementary angles.
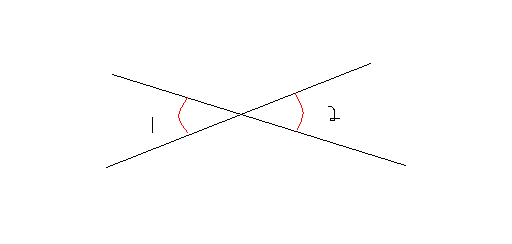
Vertical angles:
Angles that have a common vertex and whose sides are formed by the same lines. The following(angle 1 and angle 2) are vertical angles.
When two parallel lines are crossed by a third line(Transversal), 8 angles are formed. Take a look at the following figure
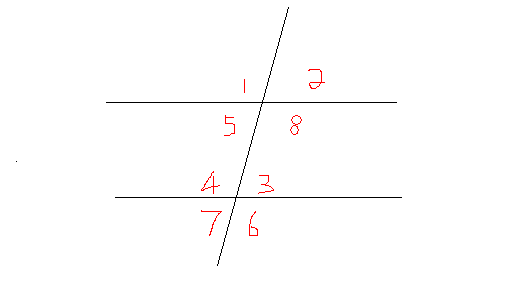
Angles 3,4,5,8 are interior angles
Angles 1,2,6,7 are exterior angles
Alternate interior angles:
Pairs of interior angles on opposite sides of the transversal.
For instance, angle 3 and angle 5 are alternate interior angles. Angle 4 and angle 8 are also alternate interior angles.
Alternate exterior angles:
Pairs of exterior angles on opposite sides of the transversal.
Angle 2 and angle 7 are alternate exterior angles.
Corresponding angles:
Pairs of angles that are in similar positions.
Angle 3 and angle 2 are corresponding angles.
Angle 5 and angle 7 are corresponding angles
An angle whose measure is less than 90 degrees. The following is an acute angle.

Right angle:
An angle whose measure is 90 degrees. The following is a right angle.

Obtuse angle:
An angle whose measure is bigger than 90 degrees but less than 180 degrees. Thus, it is between 90 degrees and 180 degrees. The following is an obtuse angle.

Straight angle
An angle whose measure is 180 degrees.Thus, a straight angle look like a straight line. The following is a straight angle.

Reflex angle:
An angle whose measure is bigger than 180 degrees but less than 360 degrees.The following is a reflex angle.

Adjacent angles:
Angle with a common vertex and one common side. <1 and <2, are adjacent angles.

Complementary angles:
Two angles whose measures add to 90 degrees. Angle 1 and angle 2 are complementary angles because together they form a right angle.
Note that angle 1 and angle 2 do not have to be adjacent to be complementary as long as they add up to 90 degrees

Supplementary angles:
Two angles whose measures add to 180 degrees. The following are supplementary angles.

Vertical angles:
Angles that have a common vertex and whose sides are formed by the same lines. The following(angle 1 and angle 2) are vertical angles.

When two parallel lines are crossed by a third line(Transversal), 8 angles are formed. Take a look at the following figure

Angles 3,4,5,8 are interior angles
Angles 1,2,6,7 are exterior angles
Alternate interior angles:
Pairs of interior angles on opposite sides of the transversal.
For instance, angle 3 and angle 5 are alternate interior angles. Angle 4 and angle 8 are also alternate interior angles.
Alternate exterior angles:
Pairs of exterior angles on opposite sides of the transversal.
Angle 2 and angle 7 are alternate exterior angles.
Corresponding angles:
Pairs of angles that are in similar positions.
Angle 3 and angle 2 are corresponding angles.
Angle 5 and angle 7 are corresponding angles
Day 4 Blog - Geometry
Activities are getting tougher as each lesson past. Now I wonder how I get through my math in primary school. I don't remember any of the strategies covered have rationale behind it. To me, it is more of imparting formulas from my teacher and we applied it accordingly to the problems.
As educators, we scaffold children's thinking and they will construct their own knowledge. Once they are able to do that, children will not forget what they had learnt.
I learnt about Pick's theorem in this session. To calculate the area of a figure drawn on a Geoboard, using Pick's theory is A = i (interior pt) + b (boundary points)/2 - 1.
Below website allowed children to explore Geoboard and apply the Pick's theorem:
http://nrich.maths.org/2883/2883
As educators, we scaffold children's thinking and they will construct their own knowledge. Once they are able to do that, children will not forget what they had learnt.
I learnt about Pick's theorem in this session. To calculate the area of a figure drawn on a Geoboard, using Pick's theory is A = i (interior pt) + b (boundary points)/2 - 1.
Below website allowed children to explore Geoboard and apply the Pick's theorem:
http://nrich.maths.org/2883/2883
Wednesday 14 August 2013
Day 3 blog - Fraction
After the 3rd lesson, I realized that every problem given, there are several ways to obtain the answer.
When we are trying out answer, usually we will work out the easiest or the method we are taught to solve a problem. But each time Dr Yeap gave a problem, the question asked was " how many ways are there to solve this problem?" Through this question, it allowed us to think of more ways to solve and "push" us to think. This is one thing which teachers can facilitate in class to allow childreb to explore other ways rather than fixtated to one way of solving a problem.
One take away from the lesson is teaching with variation and not repetition. From the example of the topic on "matching" from matching with colours, size to 3-D representation to matching objects to its use, we are able to see how progressive the topic on "Matching" are introduce with different variation. With this progressive skill, it allows teachers to better access the child's abilities.
Dr Yeap also shown example of questions the topic on fraction and how it is taught progressively from pri 2 to 6. In order for young children to learn fraction or even any Math concepts, the CPA approach is the essential methods to teach.

This book consists of Hands-on activities and colorful illustrations provide an introduction to the concepts of math and problem solving for young readers through the presentation of fun and exciting fraction problems.
When we are trying out answer, usually we will work out the easiest or the method we are taught to solve a problem. But each time Dr Yeap gave a problem, the question asked was " how many ways are there to solve this problem?" Through this question, it allowed us to think of more ways to solve and "push" us to think. This is one thing which teachers can facilitate in class to allow childreb to explore other ways rather than fixtated to one way of solving a problem.
One take away from the lesson is teaching with variation and not repetition. From the example of the topic on "matching" from matching with colours, size to 3-D representation to matching objects to its use, we are able to see how progressive the topic on "Matching" are introduce with different variation. With this progressive skill, it allows teachers to better access the child's abilities.
Dr Yeap also shown example of questions the topic on fraction and how it is taught progressively from pri 2 to 6. In order for young children to learn fraction or even any Math concepts, the CPA approach is the essential methods to teach.
This book consists of Hands-on activities and colorful illustrations provide an introduction to the concepts of math and problem solving for young readers through the presentation of fun and exciting fraction problems.
Day 2 Blog - Whole Number
Today topic was on "whole number".
My take away for today's lesson will be counting in 10s using Ten Frame. The advantages of using Ten Frames allow children to count one to one correspondence, learn number conservation as well as there visuality for children to learnt.
Once children were able to grasp the concept on "whole number", they are able to learn the rest like fraction in the same logical manner. E.g 2/4 + 1/4 = 3/4
Mathematical terms were also emphasized in today's lesson. We were taught to use the correct terms such as "less", "greater"etc when asking children to problem solve.
Below link gives us more in depth understanding on whole numbers.
http://www.nuffieldfoundation.org/sites/default/files/P2.pdf
My take away for today's lesson will be counting in 10s using Ten Frame. The advantages of using Ten Frames allow children to count one to one correspondence, learn number conservation as well as there visuality for children to learnt.
Once children were able to grasp the concept on "whole number", they are able to learn the rest like fraction in the same logical manner. E.g 2/4 + 1/4 = 3/4
Mathematical terms were also emphasized in today's lesson. We were taught to use the correct terms such as "less", "greater"etc when asking children to problem solve.
Below link gives us more in depth understanding on whole numbers.
http://www.nuffieldfoundation.org/sites/default/files/P2.pdf
Below is a link which my daughter learnt in pri 1 when she just started Math. Is so catchy till she sang non stop.
Monday 12 August 2013
Day 1 Blog
Today was the first lesson to elementary math. My initial thoughts before the lesson is to gather as much information on ways to teach Mathematics. However, after today's lesson, i understand more on the syllabus by MOE and my take away is on how children learnt Mathematics instead.
From the first problem solving using Tangrams, we as learners gathered that we learnt through exploration, scaffolding and role modelling. Thus, children learned through the above ways too.
My daughter is currently in primary two and teaching her Math is a daunting task for me. I ended up scolding or screaming at her most of the time instead of teaching her due to my frustration why she couldn't grasp the concepts.
After today's class, I had a realisation that I do not understand how she learnt. Dr Yeap mentioned that besides the three methods listed earlier, children learnt through using concrete materials, pictorial and abstract. My mistake would be teaching my daughter using pictorial (bar model) and hoping she is able to grasp the concept (abstract).
I enjoyed all the problems posed today. Though it is elementary mathematics, but it kept us thinking and challenged us to problem solve in many ways.
From the first problem solving using Tangrams, we as learners gathered that we learnt through exploration, scaffolding and role modelling. Thus, children learned through the above ways too.
My daughter is currently in primary two and teaching her Math is a daunting task for me. I ended up scolding or screaming at her most of the time instead of teaching her due to my frustration why she couldn't grasp the concepts.
After today's class, I had a realisation that I do not understand how she learnt. Dr Yeap mentioned that besides the three methods listed earlier, children learnt through using concrete materials, pictorial and abstract. My mistake would be teaching my daughter using pictorial (bar model) and hoping she is able to grasp the concept (abstract).
I enjoyed all the problems posed today. Though it is elementary mathematics, but it kept us thinking and challenged us to problem solve in many ways.
Saturday 10 August 2013
Chapter 1 & 2
Dear Parents,
Welcome to our first E Mathematics Newsletter!
Let's recall...
(1) Do you fear of the subject Math when you were young?
(2) Do you feel uneasy at the sight of numbers and symbols?
(3) Are you concern about your child doing Math?
Fear Not! In this issue, you will understand more about what your child will be learning on Math Education.
There are 6 principles that are fundamental to high quality mathematical education. It allows us to understand math education is more than just learning the content and its objectives.
Our children learn mathematics by going through the 5 process standards:
(1) Problem Solving
(2) Reasoning and Proof
(3) Communication
(4) Connections
(5) Representation
The principles and standards also provides guidance and directions for teachers in math education.
Do you know that Mathematics has a pattern of regularity and is in logical order?
Doing Mathematics takes time and effort for both children and teachers as we need to generate strategies for solving problem, applying it for solutions as well as checking if the answer make sense.
As Math Teachers, it is important that we bring fun to it by doing it hands on! Introducing concepts to children through different tools such as countable objects, unifix cubes, spinner, rod etc...
So let's not fear of Mathematics, instead, embrace it with confidence and fun!
Welcome to our first E Mathematics Newsletter!
Let's recall...
(1) Do you fear of the subject Math when you were young?
(2) Do you feel uneasy at the sight of numbers and symbols?
(3) Are you concern about your child doing Math?
Fear Not! In this issue, you will understand more about what your child will be learning on Math Education.
There are 6 principles that are fundamental to high quality mathematical education. It allows us to understand math education is more than just learning the content and its objectives.
Our children learn mathematics by going through the 5 process standards:
(1) Problem Solving
(2) Reasoning and Proof
(3) Communication
(4) Connections
(5) Representation
The principles and standards also provides guidance and directions for teachers in math education.
Do you know that Mathematics has a pattern of regularity and is in logical order?
Doing Mathematics takes time and effort for both children and teachers as we need to generate strategies for solving problem, applying it for solutions as well as checking if the answer make sense.
As Math Teachers, it is important that we bring fun to it by doing it hands on! Introducing concepts to children through different tools such as countable objects, unifix cubes, spinner, rod etc...
So let's not fear of Mathematics, instead, embrace it with confidence and fun!
Subscribe to:
Posts (Atom)


